Exactly or Nearly the Same Again

Geometric problem

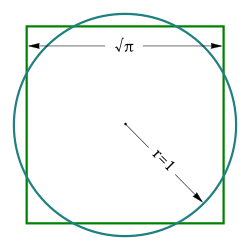
Squaring the circle: the areas of this square and this circle are both equal to π. In 1882, it was proven that this figure cannot exist synthetic in a finite number of steps with an idealized compass and straightedge.

Some credible partial solutions gave false promise for a long fourth dimension. In this figure, the shaded figure is the Lune of Hippocrates. Its area is equal to the area of the triangle ABC (found by Hippocrates of Chios).

Squaring the circle is a problem proposed by ancient geometers. It is the challenge of constructing a square with the aforementioned area as a given circle past using only a finite number of steps with compass and straightedge. The difficulty of the trouble raised the question of whether specified axioms of Euclidean geometry concerning the existence of lines and circles implied the existence of such a foursquare.

In 1882, the task was proven to be impossible, every bit a consequence of the Lindemann–Weierstrass theorem, which proves that pi (π) is a transcendental, rather than an algebraic irrational number; that is, it is non the root of any polynomial with rational coefficients. It had been known for decades that the construction would be impossible if π were transcendental, merely π was not proven to exist transcendental until 1882. Guess squaring to whatsoever given non-perfect accurateness, in dissimilarity, is possible in a finite number of steps, since in that location are rational numbers arbitrarily close to π.

The expression "squaring the circle" is sometimes used as a metaphor for trying to do the incommunicable.^[1]

The term quadrature of the circle is sometimes used to mean the same thing as squaring the circumvolve, merely it may also refer to guess or numerical methods for finding the expanse of a circle.

History [edit]

Methods to approximate the area of a given circumvolve with a foursquare, which can be thought of every bit a precursor trouble to squaring the circle, were known already to Babylonian mathematicians. The Egyptian Rhind papyrus of 1800 BC gives the area of a circle every bit 64 / 81 d  ⁱⁱ, where d is the diameter of the circumvolve. In modern terms, this is equivalent to approximating π as 256 / 81 (approximately iii.1605), a number that appears in the older Moscow Mathematical Papyrus and is used for volume approximations (east.k. hekat). Indian mathematicians also found an approximate method, though less accurate, documented in the Shulba Sutras.^[2] Archimedes proved the formula for the surface area of a circle ( A = π r ² , where r is the radius of the circle) and showed that the value of π lay between iii+ 1 / vii (approximately 3.1429) and 3+ ten / 71 (approximately 3.1408). Come across Numerical approximations of π for more on the history.

The first known Greek to be associated with the trouble was Anaxagoras, who worked on it while in prison. Hippocrates of Chios squared certain lunes, in the hope that it would lead to a solution – see Lune of Hippocrates. Retort the Sophist believed that inscribing regular polygons within a circumvolve and doubling the number of sides will eventually fill up up the expanse of the circle, and since a polygon can exist squared, it means the circle tin be squared. Even and so there were skeptics—Eudemus argued that magnitudes cannot be divided up without limit, so the area of the circle will never exist used up.^[3] The problem was even mentioned in Aristophanes'south play The Birds.

Information technology is believed that Oenopides was the offset Greek who required a airplane solution (that is, using simply a compass and straightedge). James Gregory attempted a proof of its impossibility in Vera Circuli et Hyperbolae Quadratura (The True Squaring of the Circle and of the Hyperbola) in 1667.^[4] Although his proof was faulty, it was the start paper to attempt to solve the problem using algebraic backdrop of π. It was not until 1882 that Ferdinand von Lindemann rigorously proved its impossibility.

The Victorian-age mathematician, logician, and author Charles Lutwidge Dodgson, better known past the pseudonym Lewis Carroll, also expressed interest in debunking casuistic circle-squaring theories. In i of his diary entries for 1855, Dodgson listed books he hoped to write including 1 called "Patently Facts for Circle-Squarers". In the introduction to "A New Theory of Parallels", Dodgson recounted an attempt to demonstrate logical errors to a couple of circle-squarers, stating:^[vi]

The start of these 2 misguided visionaries filled me with a slap-up ambition to do a feat I have never heard of equally accomplished by man, namely to convince a circumvolve squarer of his error! The value my friend selected for Pi was 3.2: the enormous fault tempted me with the idea that it could exist easily demonstrated to Exist an fault. More than a score of letters were interchanged before I became sadly convinced that I had no take chances.

A ridiculing of circle-squaring appears in Augustus de Morgan's A Upkeep of Paradoxes published posthumously by his widow in 1872. Having originally published the work every bit a series of manufactures in the Athenæum, he was revising it for publication at the time of his death. Circle squaring was very popular in the nineteenth century, simply inappreciably anyone indulges in it today and it is believed that de Morgan's work helped bring this about.^[7]

The 2 other classical problems of antiquity, famed for their impossibility, were doubling the cube and trisecting the angle. Like squaring the circle, these cannot exist solved by compass-and-straightedge methods. However, unlike squaring the circle, they can be solved past the slightly more powerful construction method of origami, as described at mathematics of paper folding.

Impossibility [edit]

The solution of the trouble of squaring the circle past compass and straightedge requires the construction of the number √ π . If √ π is constructible, information technology follows from standard constructions that π would also be constructible. In 1837, Pierre Wantzel showed that lengths that could be constructed with compass and straightedge had to be solutions of certain polynomial equations with rational coefficients.^{[eight] [9]} Thus, constructible lengths must be algebraic numbers. If the problem of the quadrature of the circumvolve could be solved using only compass and straightedge, and so π would have to be an algebraic number. Johann Heinrich Lambert conjectured that π was not algebraic, that is, a transcendental number, in 1761.^[ten] He did this in the same paper in which he proved its irrationality, even before the general beingness of transcendental numbers had been proven. It was not until 1882 that Ferdinand von Lindemann proved the transcendence of π and so showed the impossibility of this construction.^[eleven]

The transcendence of π implies the impossibility of exactly "circling" the square, equally well as of squaring the circle.

It is possible to construct a foursquare with an expanse arbitrarily close to that of a given circle. If a rational number is used as an approximation of π, then squaring the circle becomes possible, depending on the values called. Notwithstanding, this is only an approximation and does not meet the constraints of the ancient rules for solving the trouble. Several mathematicians have demonstrated workable procedures based on a variety of approximations.

Angle the rules by introducing a supplemental tool, assuasive an infinite number of compass-and-straightedge operations or by performing the operations in certain non-Euclidean geometries likewise makes squaring the circle possible in some sense. For case, the quadratrix of Hippias provides the means to foursquare the circumvolve and also to trisect an arbitrary angle, as does the Archimedean screw.^[12] Although the circle cannot exist squared in Euclidean space, it sometimes can be in hyperbolic geometry under suitable interpretations of the terms.^{[13] [fourteen]} Every bit there are no squares in the hyperbolic aeroplane, their part needs to be taken by regular quadrilaterals, meaning quadrilaterals with all sides congruent and all angles congruent (but these angles are strictly smaller than correct angles). There exist, in the hyperbolic airplane, (countably) infinitely many pairs of constructible circles and constructible regular quadrilaterals of equal area, which, however, are synthetic simultaneously. At that place is no method for starting with a regular quadrilateral and constructing the circumvolve of equal area, and there is no method for starting with a circle and constructing a regular quadrilateral of equal area (even when the circle has small enough radius such that a regular quadrilateral of equal area exists).

Mod approximative constructions [edit]

Though squaring the circle with perfect accuracy is an incommunicable problem using only compass and straightedge, approximations to squaring the circumvolve can exist given past amalgam lengths close toπ. It takes only minimal knowledge of unproblematic geometry to convert any given rational approximation of π into a respective compass-and-straightedge construction, but constructions made in this way tend to be very long-winded in comparison to the accuracy they reach. After the exact problem was proven unsolvable, some mathematicians practical their ingenuity to finding elegant approximations to squaring the circle, defined roughly and informally equally constructions that are particularly simple amid other imaginable constructions that give like precision.

Construction past Kochański [edit]

One of the early historical approximations is Kochański's approximation which diverges from π only in the 5th decimal place. It was very precise for the time of its discovery (1685).^[fifteen]

Construction according to Kochański with continuation

In the left diagram

${\displaystyle |P_{3}P_{9}|=|P_{1}P_{ii}|{\sqrt {{\frac {twoscore}{3}}-two{\sqrt {iii}}}}\approx 3.141\,five{\color {red}33\,338}\cdot |P_{1}P_{2}|\approx \pi r.}$

Construction by Jacob de Gelder [edit]

Jacob de Gelder'southward construction with continuation

In 1849 an elegant and unproblematic construction past Jacob de Gelder (1765-1848) was published in Grünert's Archiv. That was 64 years earlier than the comparable construction by Ramanujan.^[16] Information technology is based on the approximation

${\displaystyle \pi \approx {\frac {355}{113}}=3.141\;592{\color {red}\;920\;\ldots }}$

This value is accurate to 6 decimal places and has been known in People's republic of china since the fifth century as Zu Chongzhi's fraction, and in Europe since the 17th century.

Gelder did non construct the side of the square; it was enough for him to notice the following value

${\displaystyle {\overline {AH}}={\frac {4^{2}}{7^{2}+8^{2}}}}$ .

The illustration reverse – described below – shows the construction by Jacob de Gelder with continuation.

Depict ii mutually perpendicular center lines of a circle with radius CD = 1 and make up one's mind the intersection points A and B. Lay the line segment CE = ${\displaystyle {\tfrac {7}{eight}}}$ fixed and connect Due east to A. Determine on AE and from A the line segment AF = ${\displaystyle {\tfrac {1}{two}}}$ . Depict FG parallel to CD and connect E with Thousand. Draw FH parallel to EG, then AH = ${\displaystyle {\tfrac {four^{2}}{7^{ii}+8^{2}}}.}$ Decide BJ = CB and subsequently JK = AH. Halve AK in L and use the Thales's theorem around L from A, which results in the intersection bespeak One thousand. The line segment BM is the square root of AK and thus the side length ${\displaystyle a}$ of the searched square with nearly the aforementioned surface area.

Examples to illustrate the errors:

• In a circumvolve of radius r = 100 km, the error of side length a ≈ seven.5 mm
• In the case of a circle with radius r = 1 m, the error of the area A ≈ 0.3 mm^two

Construction by Hobson [edit]

Among the mod approximate constructions was one past E. W. Hobson in 1913.^[16] This was a fairly accurate structure which was based on amalgam the approximate value of iii.14164079..., which is accurate to three decimal places (i.e. it differs from π by about four.8×10⁻⁵ ).

Hobson's construction with continuation

"Nosotros find that GH = r . 1 ^. 77246 ..., and since ${\displaystyle {\sqrt {\pi }}}$ = 1 ^. 77245 we see that GH is greater than the side of the square whose area is equal to that of the circle by less than 2 hundred thousandths of the radius."

Hobson does not mention the formula for the approximation of π in his construction. The above illustration shows Hobson'south construction with continuation.

Constructions by Ramanujan [edit]

The Indian mathematician Srinivasa Ramanujan in 1913,^{[17] [eighteen]} Carl Olds in 1963, Martin Gardner in 1966, and Benjamin Bold in 1982 all gave geometric constructions for

${\displaystyle {\frac {355}{113}}=3.141\;592{\color {carmine}\;920\;\ldots }}$

which is accurate to six decimal places ofπ.

Ramanujan'south estimate construction with the approach

355 / 113
DR is the side of the square

Sketch of "Manuscript book 1 of Srinivasa Ramanujan" p. 54

In 1914, Ramanujan gave a ruler-and-compass construction which was equivalent to taking the approximate value for π to be

${\displaystyle \left(ix^{2}+{\frac {19^{two}}{22}}\right)^{\frac {1}{four}}={\sqrt[{four}]{\frac {2143}{22}}}=3.141\;592\;65{\color {cherry}two\;582\;\ldots }}$

giving eight decimal places of π.^[xix] He describes his construction till line segment OS as follows.^[20]

"Let AB (Fig.2) exist a diameter of a circle whose middle is O. Bifurcate the arc ACB at C and trisect AO at T. Join BC and cutting off from it CM and MN equal to AT. Join AM and AN and cut off from the latter AP equal to AM. Through P draw PQ parallel to MN and meeting AM at Q. Join OQ and through T describe TR, parallel to OQ and meeting AQ at R. Describe AS perpendicular to AO and equal to AR, and join Bone. Then the mean proportional between OS and OB will be very well-nigh equal to a sixth of the circumference, the error being less than a twelfth of an inch when the bore is 8000 miles long."

In this quadrature, Ramanujan did not construct the side length of the square, it was plenty for him to show the line segment Bone. In the post-obit continuation of the structure, the line segment OS is used together with the line segment OB to represent the mean proportionals (red line segment OE).

Squaring the circumvolve, approximate construction according to Ramanujan of 1914, with continuation of the structure (dashed lines, mean proportional cherry line), come across blitheness.

Continuation of the structure up to the desired side length a of the square:

Extend AB across A and beat the circular arc b₁ around O with radius Os, resulting in Due south′. Bisect the line segment BS′ in D and describe the semicircle b₂ over D. Draw a direct line from O through C up to the semicircle b_two, information technology cuts b₂ in East. The line segment OE is the mean proportional between OS′ and OB, also called geometric hateful. Extend the line segment EO beyond O and transfer EO twice more, it results F and A₁, and thus the length of the line segment EA1 with the in a higher place described approximation value of π, the half circumference of the circle. Bisect the line segment EA_ane in Chiliad and draw the semicircle b_iii over K. Transfer the distance OB from A₁ to the line segment EA₁ , it results H. Create a vertical from H up to the semicircle b₃ on EA_i , information technology results B₁. Connect A₁ to B_i, thus the sought side a of the foursquare A_oneB₁C_oneD₁ is synthetic, which has nearly the aforementioned area as the given circumvolve.

Examples to illustrate the errors:

• In a circumvolve of radius r = ten,000 km the error of side length a ≈ −two.8 mm
• In the instance of a circle with the radius r = 10 m the error of the area A ≈ −0.1 mm²

Construction using the golden ratio [edit]

• In 1991, Robert Dixon gave a construction for

  $${\displaystyle {\frac {vi}{five}}\cdot \left(i+\varphi \correct)=3.141\;{\color {red}640\;\ldots },}$$

  

  where ${\displaystyle \varphi }$ is the golden ratio.^[21] Three decimal places are equal to those of π.
• If the radius ${\displaystyle r=one}$ and the side of the foursquare

  $${\displaystyle a={\sqrt {{\frac {6}{5}}\cdot \left(1+\varphi \right)}}={\sqrt {\varphi +1+{\frac {1}{5}}\cdot \left(1+\varphi \right)}}=i.772\;four{\color {red}67\;\ldots }}$$

  

  then the expanded 2nd formula shows the sequence of the steps for an alternative structure (see the following illustration). Four decimal places are equal to those of √ π .

Judge construction using the aureate ratio
${\displaystyle {\sqrt {{\overline {AE}}+ane+{\tfrac {1}{5}}\cdot (1+{\overline {AE}})}}={\sqrt {AG}}=a\approx {\sqrt {\pi }}}$ .

Squaring or quadrature equally integration [edit]

Finding the surface area under a bend, known as integration in calculus, or quadrature in numerical analysis, was known as squaring before the invention of calculus. Since the techniques of calculus were unknown, it was generally presumed that a squaring should be done via geometric constructions, that is, by compass and straightedge. For example, Newton wrote to Oldenburg in 1676 "I believe M. Leibnitz will not dislike the Theorem towards the beginning of my letter pag. 4 for squaring Curve lines Geometrically" (emphasis added).^[22] After Newton and Leibniz invented calculus, they notwithstanding referred to this integration problem as squaring a curve.

Claims of circle squaring [edit]

Connectedness with the longitude problem [edit]

The mathematical proof that the quadrature of the circle is impossible using but compass and straightedge has non proved to be a hindrance to the many people who have invested years in this trouble anyway. Having squared the circle is a famous crank assertion. (See also pseudomathematics.) In his old age, the English philosopher Thomas Hobbes convinced himself that he had succeeded in squaring the circle, a claim that was refuted by John Wallis equally part of the Hobbes–Wallis controversy.^{[23] [24]}

During the 18th and 19th century, the notion that the problem of squaring the circumvolve was somehow related to the longitude problem seems to accept become prevalent among would-exist circumvolve squarers. Using "cyclometer" for circumvolve-squarer, Augustus de Morgan wrote in 1872:

Montucla says, speaking of France, that he finds three notions prevalent among cyclometers: ane. That in that location is a big advantage offered for success; 2. That the longitude trouble depends on that success; 3. That the solution is the great stop and object of geometry. The same 3 notions are equally prevalent among the same class in England. No reward has always been offered by the government of either country.^[25]

Although from 1714 to 1828 the British government did indeed sponsor a £twenty,000 prize for finding a solution to the longitude problem, exactly why the connexion was fabricated to squaring the circle is not clear; especially since 2 non-geometric methods (the astronomical method of lunar distances and the mechanical chronometer) had been found by the late 1760s. The Board of Longitude received many proposals, including determining longitude by "squaring the circumvolve", though the lath did not accept "any notice" of information technology.^[26] De Morgan goes on to say that "[t]he longitude problem in no manner depends upon perfect solution; existing approximations are sufficient to a point of accuracy far beyond what tin be wanted." In his book, de Morgan also mentions receiving many threatening letters from would-exist circle squarers, accusing him of trying to "crook them out of their prize".

Other modern claims [edit]

Even later information technology had been proved impossible, in 1894, apprentice mathematician Edwin J. Goodwin claimed that he had developed a method to square the circle. The technique he developed did non accurately square the circle, and provided an wrong expanse of the circumvolve which essentially redefined pi as equal to 3.ii. Goodwin then proposed the Indiana Pi Bill in the Indiana land legislature allowing the state to use his method in education without paying royalties to him. The bill passed with no objections in the state house, but the bill was tabled and never voted on in the Senate, amid increasing ridicule from the press.^[27]

The mathematical crank Carl Theodore Heisel also claimed to have squared the circumvolve in his 1934 book, "Behold! : the grand trouble no longer unsolved: the circle squared beyond refutation."^[28] Paul Halmos referred to the volume as a "classic crank volume."^[29]

In 1851, John Parker published a book Quadrature of the Circle in which he claimed to have squared the circle. His method really produced an approximation of π authentic to 6 digits.^{[30] [31] [32]}

In literature [edit]

J. P. de Faurè, Dissertation, découverte, et demonstrations de la quadrature mathematique du cercle, 1747

The problem of squaring the circumvolve has been mentioned past poets such as Dante and Alexander Pope, with varied metaphorical meanings. Its literary employ dates dorsum at least to 414 BC, when the play The Birds past Aristophanes was first performed. In information technology, the graphic symbol Meton of Athens mentions squaring the circle, mayhap to indicate the paradoxical nature of his utopian urban center.^[33]

Dante's Paradise, canto XXXIII, lines 133–135, contain the verses:

As the geometer his mind applies
To square the circle, nor for all his wit
Finds the right formula, howe'er he tries

For Dante, squaring the circumvolve represents a task beyond human comprehension, which he compares to his own inability to comprehend Paradise.^[34]

Past 1742, when Alexander Pope published the fourth book of his Dunciad, attempts at circle-squaring had come to be seen every bit "wild and fruitless":^[31]

Mad Mathesis alone was unconfined,
Too mad for mere cloth chains to bind,
Now to pure space lifts her ecstatic stare,
At present, running round the circle, finds information technology square.

Similarly, the Gilbert and Sullivan comic opera Princess Ida features a song which satirically lists the impossible goals of the women'south university run by the championship character, such as finding perpetual motion. One of these goals is "And the circle – they will foursquare it/Some fine twenty-four hour period."^[35]

The sestina, a poetic form first used in the twelfth century by Arnaut Daniel, has been said to square the circle in its use of a square number of lines (six stanzas of vi lines each) with a round scheme of vi repeated words. Spanos (1978) writes that this form invokes a symbolic significant in which the circle stands for sky and the square stands for the earth.^[36] A similar metaphor was used in "Squaring the Circle", a 1908 short story past O. Henry, most a long-running family feud. In the title of this story, the circumvolve represents the natural world, while the square represents the city, the globe of man.^[37]

In later works circle-squarers such as Leopold Blossom in James Joyce'south novel Ulysses and Lawyer Paravant in Thomas Mann's The Magic Mountain are seen equally sadly deluded or as unworldly dreamers, unaware of its mathematical impossibility and making grandiose plans for a consequence they will never achieve.^{[38] [39]}

Come across also [edit]

• For a more than modern related problem, run across Tarski's circle-squaring trouble.
• The squircle is a mathematical shape with properties between those of a square and those of a circle.

References [edit]

1. ^ Ammer, Christine. "Square the Circle. Dictionary.com. The American Heritage® Dictionary of Idioms". Houghton Mifflin Company. Retrieved sixteen April 2012.
2. ^ O'Connor, John J. & Robertson, Edmund F. (2000). "The Indian Sulbasutras". MacTutor History of Mathematics archive. St Andrews Academy.
3. ^ Heath, Thomas (1981). History of Greek Mathematics . Courier Dover Publications. ISBN0-486-24074-6.
4. ^ Gregory, James (1667). Vera Circuli et Hyperbolæ Quadratura … [The truthful squaring of the circle and of the hyperbola …]. Padua: Giacomo Cadorino. Available at: ETH Bibliothek (Zürich, Switzerland)
5. ^ Cajori, Florian (1919). A History of Mathematics (2nd ed.). New York: The Macmillan Company. p. 143.
6. ^ Gardner, Martin (1996). The Universe in a Handkerchief . Springer. ISBN0-387-94673-X.
7. ^ Dudley, Underwood (1987). A Budget of Trisections. Springer-Verlag. pp. xi–xii. ISBN0-387-96568-eight. Reprinted as The Trisectors.
8. ^ Wantzel, Fifty. (1837). "Recherches sur les moyens de reconnaître si un problème de géométrie peut se résoudre avec la règle et le compas" [Investigations into means of knowing if a problem of geometry tin be solved with a straightedge and compass]. Periodical de Mathématiques Pures et Appliquées (in French). two: 366–372.
9. ^ Cajori, Florian (1918). "Pierre Laurent Wantzel". Bull. Amer. Math. Soc. 24 (seven): 339–347. doi:10.1090/s0002-9904-1918-03088-7. MR 1560082.
10. ^ Lambert, Johann Heinrich (1761). "Mémoire sur quelques propriétés remarquables des quantités transcendentes circulaires et logarithmiques" [Memoir on some remarkable backdrop of circular transcendental and logarithmic quantities]. Histoire de fifty'Académie Royale des Sciences et des Belles-Lettres de Berlin (in French) (published 1768). 17: 265–322.
11. ^ Lindemann, F. (1882). "Über dice Zahl π" [On the number π]. Mathematische Annalen (in German). twenty: 213–225. doi:10.1007/bf01446522. S2CID 120469397.
12. ^ Boyer, Carl B.; Merzbach, Uta C. (11 January 2011). A History of Mathematics. John Wiley & Sons. ISBN978-0-470-52548-7. OCLC 839010064.
13. ^ Jagy, William C. (1995). "Squaring circles in the hyperbolic plane" (PDF). Mathematical Intelligencer. 17 (two): 31–36. doi:10.1007/BF03024895. S2CID 120481094.
14. ^ Greenberg, Marvin Jay (2008). Euclidean and Non-Euclidean Geometries (4th ed.). W H Freeman. pp. 520–528. ISBN978-0-7167-9948-1.
15. ^ Weisstein, Eric Due west. "Kochanski'south Approximation". MathWorld.
16. ^ ^{a b} Hobson, Ernest William (1913). Squaring the Circle: A History of the Problem. Cambridge University Press. pp. 34–35.
17. ^ Wolfram, Stephen. "Who Was Ramanujan?". Come across as well MANUSCRIPT Book 1 OF SRINIVASA RAMANUJAN page 54 Both files were retrieved at 23 June 2016
18. ^ Castellanos, Dario (Apr 1988). "The Ubiquitous π". Mathematics Mag. 61 (2): 67–98. doi:x.1080/0025570X.1988.11977350. ISSN 0025-570X.
19. ^ Due south. A. Ramanujan: Modular Equations and Approximations to π In: Quarterly Periodical of Mathematics. 12. Some other curious approximation to π is, 43, (1914), Due south. 350–372. Listed in: Published works of Srinivasa Ramanujan
20. ^ S. A. Ramanujan: Modular Equations and Approximations to π In: Quarterly Journal of Mathematics. 12. Another curious approximation to π is ... Fig. ii, 44, (1914), Southward. 350–372. Listed in: Published works of Srinivasa Ramanujan
21. ^ Dixon, Robert A. (1 January 1991). Mathographics. Courier Corporation. ISBN978-0-486-26639-8. OCLC 22505850.
22. ^ Cotes, Roger (1850). Correspondence of Sir Isaac Newton and Professor Cotes: Including messages of other eminent men.
23. ^ Boyd, Andrew (2008). "HOBBES AND WALLIS". Episode 2372. The Engines of Our Ingenuity. Retrieved 14 November 2020.
24. ^ Bird, Alexander (1996). "Squaring the Circle: Hobbes on Philosophy and Geometry". Journal of the History of Ideas. 57 (2): 217–231. doi:10.1353/jhi.1996.0012. S2CID 171077338.
25. ^ de Morgan, Augustus (1872). A Budget of Paradoxes. p. 96.
26. ^ Lath of Longitude / Vol V / Confirmed Minutes. Cambridge University Library: Royal Observatory. 1737–1779. p. 48. Retrieved ane Baronial 2021.
27. ^ Archived at Ghostarchive and the Wayback Machine: Numberphile (12 March 2013), How Pi was nearly inverse to iii.2 - Numberphile
28. ^ Heisel, Carl Theodore (1934). Behold! : the grand trouble the circle squared across refutation no longer unsolved. Heisel.
29. ^ Paul R. Halmos (1970). "How to Write Mathematics". Fifty'Enseignement mathématique. 16 (two): 123–152. — Pdf
30. ^ Beckmann, Petr (2015). A History of Pi. St. Martin's Press. p. 178. ISBN9781466887169.
31. ^ ^{a b} Schepler, Herman C. (1950). "The chronology of pi". Mathematics Magazine. 23 (3): 165–170, 216–228, 279–283. doi:10.2307/3029284. JSTOR 3029832. MR 0037596.
32. ^ Abeles, Francine F. (1993). "Charles L. Dodgson's geometric approach to arctangent relations for pi". Historia Mathematica. 20 (2): 151–159. doi:ten.1006/hmat.1993.1013. MR 1221681.
33. ^ Amati, Matthew (2010). "Meton's star-city: Geometry and utopia in Aristophanes' Birds". The Classical Periodical. 105 (3): 213–222. doi:10.5184/classicalj.105.three.213. JSTOR x.5184/classicalj.105.3.213.
34. ^ Herzman, Ronald B.; Towsley, Gary B. (1994). "Squaring the circumvolve: Paradiso 33 and the poetics of geometry". Traditio. 49: 95–125. doi:10.1017/S0362152900013015. JSTOR 27831895.
35. ^ Dolid, William A. (1980). "Vivie Warren and the Tripos". The Shaw Review. 23 (2): 52–56. JSTOR 40682600. Dolid contrasts Vivie Warren, a fictional female person mathematics educatee in Mrs. Warren's Profession by George Bernard Shaw, with the satire of higher women presented by Gilbert and Sullivan. He writes that "Vivie naturally knew better than to try to square circles."
36. ^ Spanos, Margaret (1978). "The Sestina: An Exploration of the Dynamics of Poetic Structure". Speculum. 53 (3): 545–557. doi:10.2307/2855144. JSTOR 2855144. S2CID 162823092.
37. ^ Blossom, Harold (1987). Twentieth-century American literature. Chelsea Business firm Publishers. p. 1848. ISBN9780877548034. Similarly, the story "Squaring the Circle" is permeated with the integrating image: nature is a circumvolve, the city a foursquare.
38. ^ Pendrick, Gerard (1994). "Ii notes on "Ulysses"". James Joyce Quarterly. 32 (ane): 105–107. JSTOR 25473619.
39. ^ Goggin, Joyce (1997). The Large Deal: Card Games in 20th-Century Fiction (PhD). Academy of Montréal. p. 196.

External links [edit]

• Media related to Squaring the circumvolve at Wikimedia Commons

• Squaring the circumvolve at the MacTutor History of Mathematics archive
• Squaring the Circle at cut-the-knot
• Circle Squaring at MathWorld, includes information on procedures based on various approximations of pi
• "Squaring the Circle" at "Convergence"
• The Quadrature of the Circle and Hippocrates' Lunes at Convergence
• How to Unroll a Circumvolve Pi accurate to viii decimal places, using straightedge and compass.
• Squaring the Circle and Other Impossibilities, lecture by Robin Wilson, at Gresham College, sixteen January 2008 (available for download as text, audio or video file).
• Archived at Ghostarchive and the Wayback Machine: Grime, James. "Squaring the Circle". Numberphile. Brady Haran.
• "2000 years unsolved: Why is doubling cubes and squaring circles impossible?" by Burkard Polster

realemagain.blogspot.com

Source: https://en.wikipedia.org/wiki/Squaring_the_circle